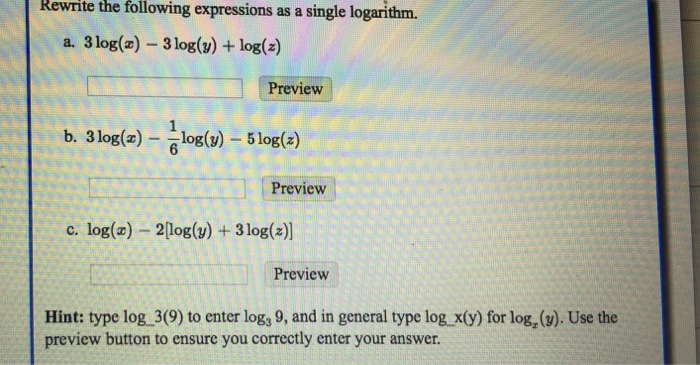
Rewrite the following expressions as a single logarithm: Embark on an intellectual journey as we delve into the captivating world of logarithms and their remarkable ability to simplify complex expressions into a unified representation.
Logarithms, with their inherent properties, provide a powerful tool for condensing and transforming mathematical expressions, offering a streamlined approach to solving equations and simplifying calculations.
Rewriting Expressions as a Single Logarithm

Logarithms are mathematical operations that express a number as the exponent of a base. Rewriting expressions as a single logarithm involves combining multiple logarithmic terms into a single term with the same base and argument.
Methods for Rewriting Expressions, Rewrite the following expressions as a single logarithm
- Product Rule:log a(xy) = log a(x) + log a(y)
- Quotient Rule:log a(x/y) = log a(x) – log a(y)
- Power Rule:log a(x n) = n log a(x)
Examples of Rewriting Expressions
| Original Expression | Product Rule | Quotient Rule | Power Rule |
|---|---|---|---|
| log2(6) + log2(5) | log2(30) | – | – |
log10(100)
|
– | log10(2) | – |
| log3(81) | – | – | 4 log3(3) |
Applications of Rewriting Expressions
Rewriting expressions as a single logarithm simplifies calculations and solves equations and inequalities. For instance, to solve log 10(x) + log 10(y) = 1, rewrite the expression as log 10(xy) = 1, then solve for xy.
In real-world applications, rewriting expressions is useful in finance, engineering, and scientific research.
Additional Considerations
Rewriting expressions has limitations, such as not always being possible or simplifying the expression. It’s crucial to understand the underlying mathematical concepts and avoid common errors, such as using incorrect rules or making algebraic mistakes.
Essential Questionnaire: Rewrite The Following Expressions As A Single Logarithm
What are the benefits of rewriting expressions as a single logarithm?
Rewriting expressions as a single logarithm offers several advantages, including simplified calculations, efficient equation solving, and a deeper understanding of logarithmic relationships.
How can I apply the product rule of logarithms to rewrite expressions?
The product rule of logarithms states that the logarithm of a product is equal to the sum of the logarithms of the individual factors. For example, log(ab) = log(a) + log(b).
What is the significance of the power rule of logarithms?
The power rule of logarithms states that the logarithm of a number raised to a power is equal to the power multiplied by the logarithm of the number. For example, log(a^n) = n – log(a).