In the realm of mathematics, factorization reigns supreme as a fundamental tool for simplifying and solving algebraic expressions. As we delve into the intricacies of write each power as a product of the same factor, we embark on an intellectual adventure that unravels the secrets of expression manipulation.
Through the lens of exponents and common factors, we uncover the hidden patterns within complex expressions. By harnessing the power of factorization, we gain the ability to dissect algebraic equations, unlocking their secrets and revealing their underlying structures.
Factorization of Algebraic Expressions
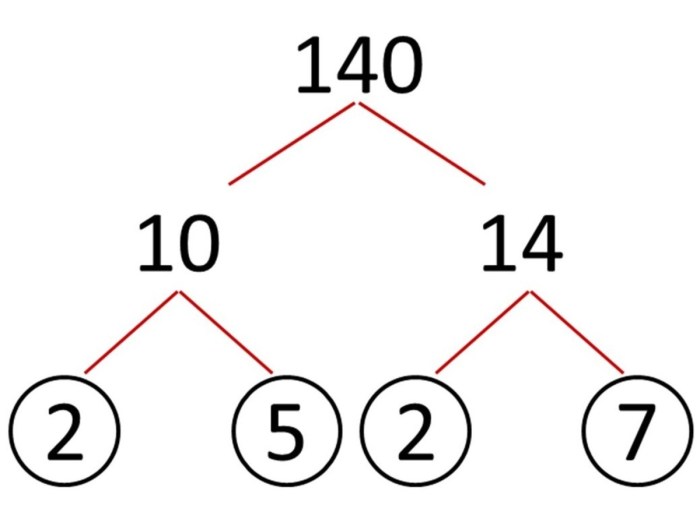
Factorization is the process of breaking down an algebraic expression into smaller, simpler expressions. This process is useful for simplifying expressions, solving equations, and finding the greatest common factor (GCF) and least common multiple (LCM) of two or more expressions.
Examples of Factorization
- x 2– 9 = (x + 3)(x – 3)
- x 2+ 5x + 6 = (x + 2)(x + 3)
- x 3– 8 = (x – 2)(x 2+ 2x + 4)
Process of Factoring, Write each power as a product of the same factor
There are several methods for factoring algebraic expressions, including:
- Factoring by grouping
- Factoring by using the difference of squares formula
- Factoring by using the sum or difference of cubes formula
Prime Factorization
Definition of Prime Factorization
Prime factorization is the process of breaking down a number into its prime factors. A prime factor is a number that can only be divided by itself and 1.
Steps Involved in Prime Factorization
- Divide the number by the smallest prime number that divides it evenly.
- Continue dividing the resulting number by the smallest prime number that divides it evenly.
- Repeat step 2 until the resulting number is 1.
Examples of Prime Factorization
- 12 = 2 x 2 x 3
- 25 = 5 x 5
- 100 = 2 x 2 x 5 x 5
Exponents and Factorization: Write Each Power As A Product Of The Same Factor
Exponents can be used to factor expressions by converting them into products of the same factor. For example, the expression x 2– 4 can be factored as (x + 2)(x – 2) by using the exponent 2.
Examples of Factoring Using Exponents
- x 3– 8 = (x – 2)(x 2+ 2x + 4)
- x 4– 16 = (x 2+ 4)(x 2– 4)
- x 5– 32 = (x – 2)(x 4+ 2x 3+ 4x 2+ 8x + 16)
Common Factors and Multiples
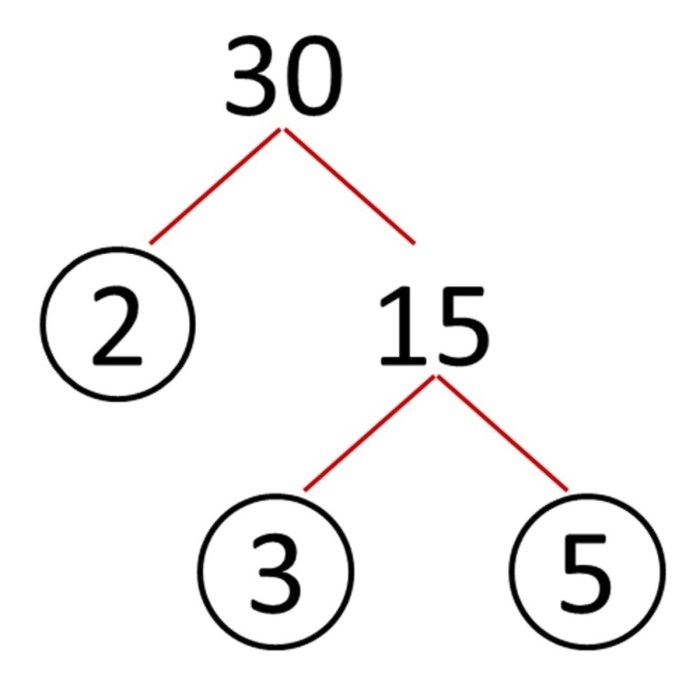
Definition of Common Factors and Multiples
Common factors are the factors that two or more numbers have in common. Common multiples are the multiples that two or more numbers have in common.
Finding the GCF and LCM
The greatest common factor (GCF) of two or more numbers is the largest factor that divides all of the numbers evenly. The least common multiple (LCM) of two or more numbers is the smallest multiple that is divisible by all of the numbers.
Applications of Factorization
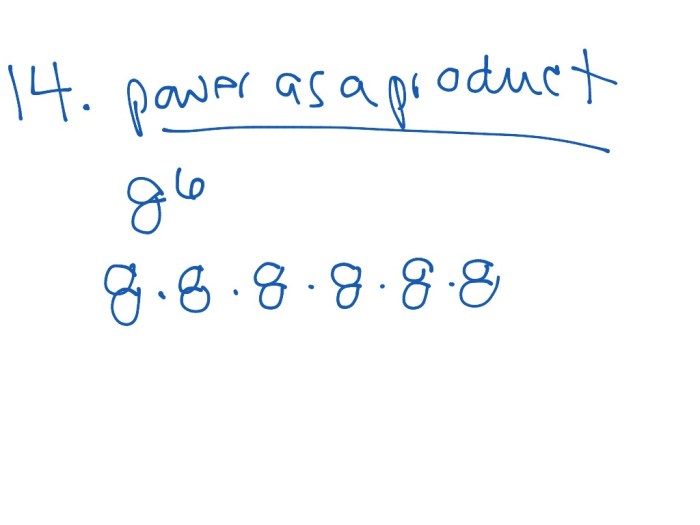
Factorization has many applications in mathematics, including:
- Solving equations
- Simplifying expressions
- Finding the GCF and LCM of two or more numbers
Solving Equations
Factorization can be used to solve equations by setting each factor equal to zero and solving for the variable.
Simplifying Expressions
Factorization can be used to simplify expressions by combining like terms.
Question Bank
What is the significance of factorization in mathematics?
Factorization is a fundamental technique that allows us to decompose algebraic expressions into simpler building blocks, revealing their underlying structure and simplifying complex equations.
How does write each power as a product of the same factor relate to exponents?
By expressing each power as a product of the same factor, we can leverage the laws of exponents to simplify and manipulate algebraic expressions, making them more manageable and easier to solve.
What are the practical applications of factorization?
Factorization finds widespread application in various fields, including solving equations, simplifying expressions, finding common denominators, and analyzing polynomials.